MA301BS: MATHEMATICS - IV
(Complex Variables and Fourier Analysis)
B.Tech. II Year I Sem. L T P C
4 1 0 4

---

Prerequisites: Foundation course (No Prerequisites).

Course Objectives: To learn

• differentiation and integration of complex valued functions
• evaluation of integrals using Cauchy’s integral formula
• Laurent’s series expansion of complex functions
• evaluation of integrals using Residue theorem
• express a periodic function by Fourier series and a non-periodic function by Fourier transform
• to analyze the displacements of one dimensional wave and distribution of one dimensional heat equation

Course Outcomes: After learning the contents of this paper the student must be able to:

• analyze the complex functions with reference to their analyticity, integration using Cauchy’s integral theorem
• find the Taylor’s and Laurent’s series expansion of complex functions
• the bilinear transformation
• express any periodic function in term of sines and cosines
• express a non-periodic function as integral representation
• analyze one dimensional wave and heat equation

UNIT – I

Functions of a complex variable: Introduction, Continuity, Differentiability, Analyticity, properties, Cauchy, Riemann equations in Cartesian and polar coordinates. Harmonic and conjugate harmonic functions-Milne-Thompson method

UNIT - II

Complex integration: Line integral, Cauchy’s integral theorem, Cauchy’s integral formula, and Generalized Cauchy’s integral formula, Power series: Taylor’s series- Laurent series, Singular points, isolated singular points, pole of order m – essential singularity, Residue, Cauchy Residue theorem (Without proof).

UNIT – III

Evaluation of Integrals: Types of real integrals:
a) Improper real integrals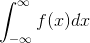

(b)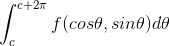 

Bilinear transformation- fixed point- cross ratio- properties- invariance of circles.

UNIT – IV

Fourier series and Transforms: Introduction, Periodic functions, Fourier series of periodic function, Dirichlet’s conditions, Even and odd functions, Change of interval, Half range sine and cosine series.
Fourier integral theorem (without proof), Fourier sine and cosine integrals, sine and cosine, transforms, properties, inverse transforms, Finite Fourier transforms.

UNIT – V

Applications of PDE: Classification of second order partial differential equations, method of separation of variables, Solution of one dimensional wave and heat equations.

TEXT BOOKS:

1. A first course in complex analysis with applications by Dennis G. Zill and Patrick Shanahan, Johns and Bartlett Publishers.
2. Higher Engineering Mathematics by Dr. B. S. Grewal, Khanna Publishers.
3. Advanced engineering Mathematics with MATLAB by Dean G. Duffy

REFERENCES:

1. Fundamentals of Complex Analysis by Saff, E. B. and A. D. Snider, Pearson.
2. Advanced Engineering Mathematics by Louis C. Barrett, McGraw Hill.